Arity Science

Compositional Structure of Higher-Order Systems

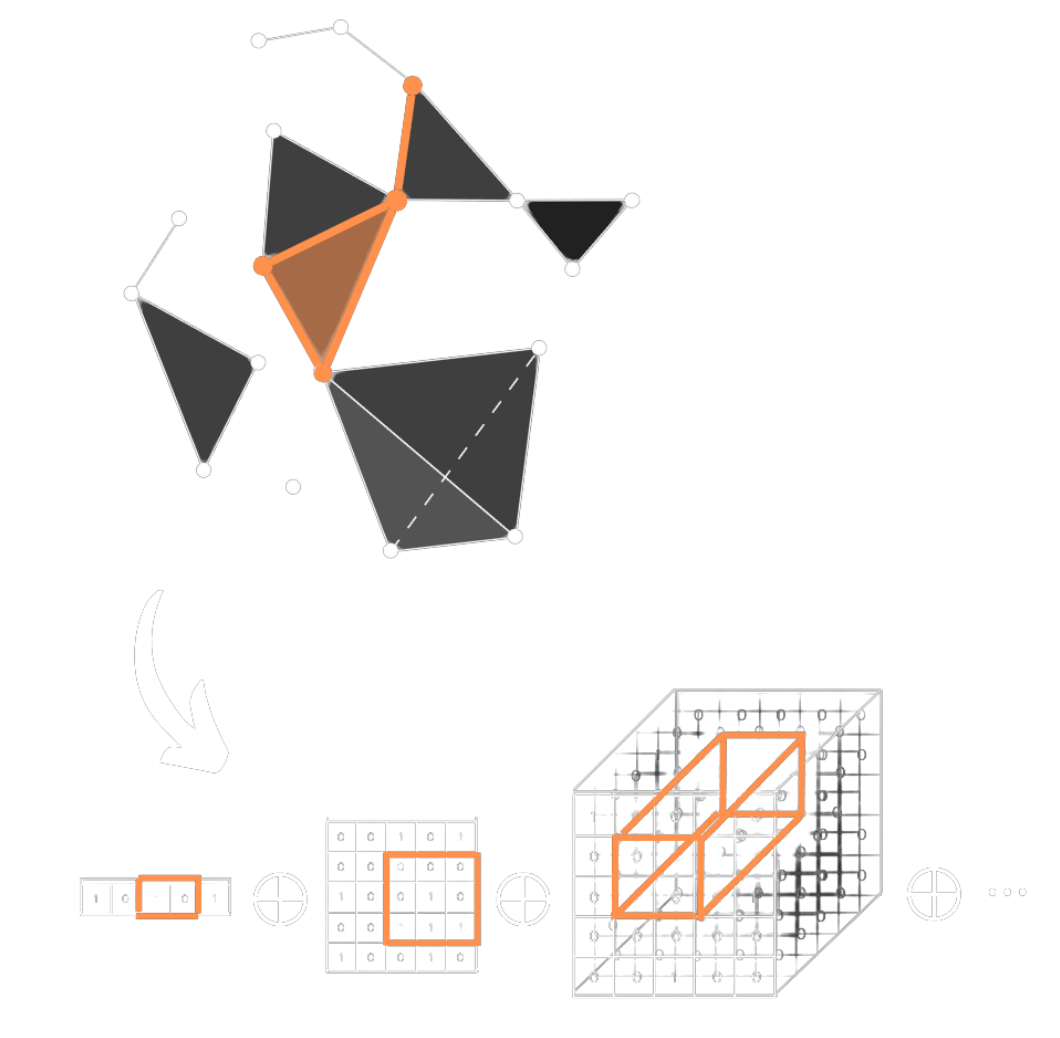
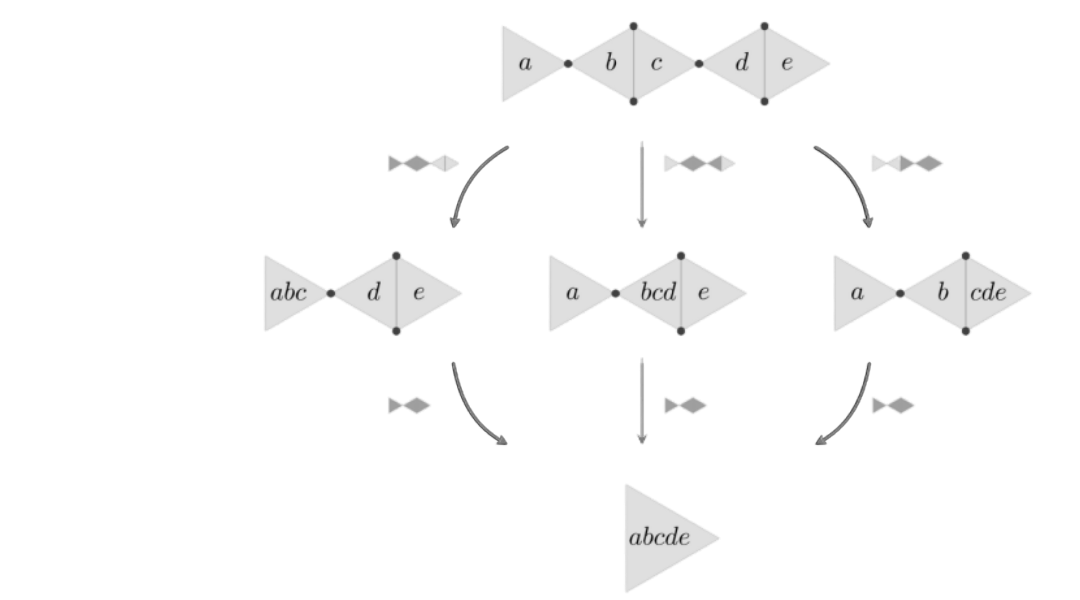
Arity Science is a multi-project research programme that aims to develop novel mathematical and computational frameworks, generalizing existing formalisms such as category theory, relational algebra and network theory, that can accommodate the complexity of higher-order systems while remaining rigorous and computable. Arity Science is a transdisciplinary effort that focuses on the formal investigation of mathematical objects such as n-ary algebras or hypergraphs, and their subsequent application for the modelling of higher-order phenomena across scientific disciplines, including brain connectomics, rewriting and automata, genome topology, art history or molecular computing.

"The task is not to see what has never been seen before,
but to think what has never been thought before about what we see everyday"
Erwin Schrödinger

Goals

Characterize Complexity from Arity. Many complex systems such as ecosystems, societies or cells, involve mechanisms that go beyond pairwise interactions leading to higher-order emergent and non-linear phenomena. What is the impact of the arity of interaction on the complex behaviour of a system?

Survey Irreducible Arity. The Borromean rings, a configuration of three loops in space that are linked while not being pairwise linked, represent the paradigmatic example of an irreducible ternary relation. The phenomenon of irreducible arity is likely ubiquitous across mathematics and science.

Formalize Hypergraph Adjacency. There is a well-known connection between graph theory and linear algebra, most notably exploited in network theory, based on the concept of adjacency. A hypergraph analogue of such a connection, which would involve hypermatrix algebra, has not been described in full detail and it is likely to prove instrumental in the modelling of higher-order systems.

Develop Non-Sequential Computation. The notion of sequence, both abstract (a tuple) and practical (processes in minds and machines), dominates the current landscape of mathematical and computational formalisms. Higher-order phenomena call for a systematic framework that implements non-binary and non-sequential notions of operations, transformations and processes.

Define Higher-Arity Categories. Category theory, with the notion of directed (binary) morphism at the core, is generally regarded to capture fundamental structural features of large areas of mathematics. Surprisingly, very little work exists on the notion of higher-arity morphisms and the use of hypergraphs as models for commutative diagrams. Examples from matrix theory and ternary algebra, however, point towards a rich compositional structure in higher-arity categories.

Explore Higher Algebra. A vast landscape of n-ary, non-sequential and hypercompositional algebraic structures remains unexplored due to a combination of historical biases, human cognitive limitations and technical challenges. Novel approaches using hypergraphs and computer-aided notation are revealing previously unseen patterns.

People

Timeline

21/10/2024 - [Published Article] - "Diagrammatic calculus and generalized associativity for higher-arity tensor operations" in Theoretical Computer Science, Elsevier.

21/06/2024 - [Talk] - "Hypergraph Rewriting Systems for Theory Enumeration and Discovery" at the Bridging Formal and Informal Mathematics conference at the Hausdorff Research Institute, Boon .

21/06/2024 - [Talk] - "New Mathematics for Higher-Order Networks" at the Network Science 2024 conference, Quebec.

27/05/2024 - [Workshop] - HyperMatrix Workshop II, Paris. A gathering of researchers working on different branches of mathematics, computer science and physics united under the theme of generalized matrix algebra and higher-order structures.

19/12/2023 - [Meeting] - Carlos and Josh meet to start discussions about the Bhattacharya-Mesner Product.

15/09/2023 - [Published Article] - "Hypermatrix Algebra and Irreducible Arity in Higher-Order Systems" in Advances in Complex Systems, World Scientific.

09/08/2023 - [Published Article] - "Biunit pairs in semiheaps and associated semigroups" in Semigroup Forum Journal, Springer

24/07/2023 - [Course] - "Foundations of Mathematics and Hypernetwork Theory" at the SEMF Interdisciplinary Summer School 2023

14/07/2023 - [Talk] - "Hypergraph Rewriting and Higher-Arity Algebra" at the Software Technologies: Applications and Foundations 2023 conference, Leicester.

14/07/2023 - [Talk] - "Higher-Arity Algebra for Higher-Order Networks" at the Network Science 2023 conference, Vienna.

24/04/2023 - [Workshop] - HyperMatrix Workshop I, online. A gathering of researchers working on different branches of mathematics, computer science and physics united under the theme of generalized matrix algebra and higher-order structures.

07/02/2023 - [Software] - Carlos begins work with Nik Murzin on the development and implementation of a hypergraph rewriting and hypermatrix algebra function package.

05/01/2023 - [Paper] - Beyond Binary: Hypermatrix Algebra and Irreducible Arity in Higher-Order Systems.

20/12/2022 - [Talk] - "Chemoids and n-ary associativity" at the 10th Symposium on Compositional Structures, Edinburgh.

03/12/2022 - [Workshop] - Ternary Day Edinburgh 2022, 2nd Edition - a workshop on ternary and higher-arity structures in algebra, geometry and category theory bringing together mathematicians, physicists and computer scientists.

15/09/2022 - [Paper] - "Biunit pairs in semiheaps and associated semigroups"

09/09/2022 - [Talk] - "The Hyperconnected World" at Topology, Physics and Chemistry 2022, EUTOPIA COST Action

08/09/2022 - [Meeting] - Carlos, Luca and Gianmarco meet in Trento to begin work on neuron-glia connectivity

25/07/2022 - [Meeting] - Carlos and Adrés meet in Valencia to begin work on higher-arity categories

28/07/2022 - [Talk] - "Non-Binary Mathematics" at the ENEM Conference 2022

18/07/2022 - [Course] - "Introduction to Hypergraphs and Category Theory" at the SEMF Interdisciplinary Summer School 2022

06/07/2022 - [Meeting] - Carlos and Davide meet in Edinburgh to begin work on genome connectivity

17/06/2022 - [Workshop] - Ternary Day Edinburgh 2022 1st Edition - a workshop on ternary and higher-arity structures in algebra, geometry and category theory bringing together mathematicians, physicists and computer scientists.

01/05/2022 - [Paper] - "Heaps of Fish: arrays, generalized associativity and heapoids"

27/04/2022 - [Meeting] - Bernard and Carlos meet for the first time in Edinburgh and begin collaboration on ternary algebra

13/04/2022 - [Talk] - "Higher Arity Mathematics" at the Wolfram Physics Seminar

23/03/2022 - [Talk] - "3-Lie Algebras, Heaps and the Mystery of Ternary Associativity" at the North British Mathematical Physics Seminar

28/02/2022 - [Meeting] - Tali and Carlos meet in Cape Town to work on plex algebra and discuss the Arity Science project at large

21/01/2022 - [Paper] - "An invitation to Higher Arity Science"

16/12/2021 - [Meeting] - Carlos and Xerxes meet in Barcelona to discuss the fish structure

15/07/2021 - [Meeting] - Xerxes, Tali and Carlos meet for the first time at the Wolfram Summer School and Carlos presents the Arity Science project there

26/11/2020 - [Talk] - "The Need for Ternary Categories" at the Edinburgh Category Theory Seminar

29/04/2020 - [Origins] - Carlos becomes interested in 3-Lie algebras and ternary associativity following conversations with José Figueroa-O'Farrill in Edinburgh

Projects

Higher-Order Connectivity in the Kinetoplast Genome

Collaboration: C. Zapata-Carratala (SEMF, WI), D. Michieletto (U. of Edinburgh)

Description: Circular DNA has been found in topologically non-trivial configurations both in vivo and in vitro. Higher-order linking structures beyond catenation, such as Borromean or Brunnian, are modelled with hypergraph adjacency. The aim is to investigate to what extent knoting and linking codifies biological information.

Output: Beyond Binary [paper], Hyperconnectivity in Topological Genomes [invited talk]

Hypernetwork Modelling for the Role of Glia in Memory Formation

Collaboration: C. Zapata-Carratala (SEMF, WI), L. Tubiana (U. of Trento), G. Zanardi (U. of Trento)

Description: Astrocytes in the human brain have been observed to bind several synapses of separate neurons in a biochemically active way. Higher-order modelling is required to perform data analytics on the brain activity patterns that may be affected by the presence of glial cells.

Output: ~research in progress~


Hypergraph Extension of Assembly Theory

Collaboration: C. Zapata-Carratala (SEMF, WI), L. Cronin (U. of Glasgow)

Description: Assembly Theory proposes a powerful model of chemical memory in an attept to systematize de biochemistry of the origin of life, among other applications. The original formulation was made in terms of simple directed graphs that were restricted to pair-wise assembly; however, directed hypergraphs were recognized to be more suited to describe assembly and they naturally account for combinations of an arbitrary number of elements.

Output: Beyond Binary [paper]


Abstract Chemistries and Higher-Arity Categories

Collaboration: C. Zapata-Carratala (SEMF, WI), A. Ortiz-Muñoz (SFI), N. Baas (NTNU)

Description: Based on the diagrammatic approach to category theory, the extension of morphisms to higher-arity bonds and the reformulation of compositional rules in terms of hypergraph rewrites leads to a natural notion of higher-arity category. These objects seem to describe general forms of abstract chemistry, which can be applied to recover concrete forms of realistic molecular reactions. Abstract chemistries are likely to play an important role in the development of the theory of molecular computing.

Output: "Ternary Categories" [talk], "Heaps of Fish: arrays, generalized associativity and heapoids" [paper], "An invitation to Higher Arity Science" [paper]


Ternary Algebra and Higher Symmetry

Collaboration: C. Zapata-Carratala (SEMF, WI), B. Rybołowicz (Heriot-Watt U.), J. Figueroa-O'Farrill (U. of Edinburgh)

Description: Ternary algebras, such as semiheaps and 3-Lie algebras, are investigated for their purely mathematical properties and the potential to generalize the notion of symmetry in physical theories. This line of research works towards the resolution of the long-standing open problem of integration of n-Leibniz algebras which can lead to insights in the generalization of gauge theories and, in particular, a better understanding of the strong nuclear force.

Output: "Associativity as Confluence" [invited talk], "Heaps of Fish: arrays, generalized associativity and heapoids" [paper], "Biunit pairs in semiheaps and associated semigroups" [paper]


Hypermatrices, Adjacency and Rewrites

Collaboration: C. Zapata-Carratala (SEMF, WI), X. Arsiwalla (U. Pompeu Fabra), T. Beynon (Wolfram Research), I. Altman (ETH Zurich)

Description: The basic mathematical theory for hypergraphs, analogous to classical graph theory, is still in its infancy. This project works towards the generalization of the basic principles of graph theory to hypergraphs and their application to network science. Particularly, higher-order adjacency in hypergraphs is modelled via hypermatrices (multi-index arrays, not to be confused with tensors) and higher-arity algebras.

Output: "Introduction to Hypergraphs" [lecture], "An invitation to Higher Arity Science" [paper], "Heaps of Fish: arrays, generalized associativity and heapoids" [paper]


Philosophy of Mathematical Creativity

Collaboration: C. Zapata-Carratala (SEMF, WI), I. Altman (ETH Zurich)

Description: The limitations of human cognition, and a combination of historical biases, have resulted in a landscape of mathematical and computational theories dominated by binary structures. As a consequence, the Arity Science effort requires a great deal of creativity and inventiveness. Philosophical enquiry and discourse that reveals preconceptions and expands methodologies is particularly useful in catalyzing the necessary ideation and imagination of new mathematics.

Output: "Non-Binary Mathematics" [invited talk], "An invitation to Higher Arity Science" [paper]